DISTRIBUCIÓN DE FRECUENCIAS PARA VARIABLES
TABLA DE DISTRIBUCIÓN DE FRECUENCIAS PARA
VARIABLES CUANTITATIVAS CONTINUAS
VARIABLES CUANTITATIVAS CONTINUAS
Uno de los primeros pasos que se realizan en un estudio estadístico es la de recoger la información ya sea por medios directos o por encuestas y agrupar los datos en una tabla denominada Tabla de distribución de frecuencias, la cual se organiza por categorías mutuamente excluyentes en las que indican el número de observaciones en cada categoría, denominado frecuencia absoluta, y otra serie de informaciones que nos permiten resumir y analizar de forma sencilla los datos a estudiar.
|
PASOS PARA CONSTRUIR UNA
TABLA DE DISTRIBUCIÓN DE FRECUENCIAS
TABLA DE DISTRIBUCIÓN DE FRECUENCIAS
No hay una regla fija que diga cual es el número de intervalos que debe tener una tabla de distribución de frecuencias, se recomienda que esté entre 5 y 15 intervalos, o podemos tener en cuenta los siguientes pasos para su construcción:
Ejemplo: Puntajes obtenidos por 80 estudiantes en una prueba.
1. Número de Intervalos: I
Los calculamos usando la fórmula de Sturges:
I = 1+3.322 Log N
En la que N es el número total de datos, por lo tanto
I = 1 + 3.322 log 80 = 7.3
Esto sugiere que el número de intervalos está alrededor de 7; por lo tanto tomaremos 8 intervalos2. Rango: R El Rango es la distancia o recorrido entre el menor valor y el mayor valor, lo calculamos así:
R = Dato Máximo - Dato Mínimo
R = 97 - 53 = 44
3. Amplitud: A
La Amplitud es el tamaño de cada intervalo, se sugiere que sean iguales; la calculamos así:
A = Rango / Número de Intervalos
A = 44/8 = 5.5
La amplitud se toma con el entero siguiente, entonces A = 6
Esto permite ampliar en Rango para que el mayor valor de los datos quede incluido en el último intervalo, de lo contrario quedaría por fuera.
4. Límites de los intervalos
Con la amplitud de 6 y el número de intervalos 8, se tiene entonces un rango más amplio 6 x 8 = 48.
Comparamos el rango inicial de 44 con este nuevo rango de 48 y observamos que lo supera en 4 unidades, este valor se divide en dos (4/2=2). Para determinar los límites de los intervalos se procede de la siguiente forma: El límite inferior del primer intervalo lo debemos iniciar desde el Dato Mínimo menos dos unidades, es decir 53 - 2 = 51. El límite inferior del segundo intervalo se calcula sumándole al anterior límite la amplitud; es decir, 51 + 6 = 57. El limite inferior del tercer intervalo será 57 + 6 = 63 y así hasta completar los demás intervalos. Nuestro primer intervalo será entonces: [51 - 57). Esta expresión indica que el límite inferior incluye al 51 y el límite superior no incluye al 57. Nuestro segundo intervalo será entonces: [57,63] y así sucesivamente...
5. frecuencia absoluta: fi
Contamos cuantos valores quedan dentro de cada intervalo.
Esta tabla presenta una desventaja de agrupación ya que aquí se pierde información, por ejemplo, en el cuarto intervalo se muestra que hay 14 estudiantes que obtuvieron un puntaje entre 69 y 75, pero no se sabe exactamente cuáles son los valores de cada uno de ellos. Esto obliga que para el cálculo posterior de las medidas de tendencia central ya no se trabaje con el intervalo de clase, sino con su promedio llamado marca de clase
6. Frecuencia relativa: Fr
Es la relación entre entre la frecuencia absoluta del intervalo y el total de las frecuencias absolutas multiplicadas por 100.
fr = (fi / N) x 100
6. frecuencia absoluta acumulada: fa
Se puede tomar en dos sentidos:
En forma ascendente contando cuántos datos hay menores que cada limite superior. En forma descendente contando cuántos datos hay mayores que cada limite inferior. Por ejemplo, para menor que, observamos que hay 1 puntaje menor que 57 puntos; hay 12 puntajes menores que 63; hay 23 puntajes menores que 69 y así sucesivamente. Por ejemplo, para mayor que, observamos que hay 80 puntajes mayores que 51; hay 79 puntajes mayores que 57; hay 68 puntajes mayores que 63 y así sucesivamente. 7. Frecuencia relativa acumulada: Fa
Como en el caso anterior, se puede tomar en dos sentidos, menor que cada límite superior o mayor que cada limite inferior; pero en términos de porcentaje.
A manera de ejemplo mostraré la interpretación de cada valor, escrito en rojo en la tabla anterior: 20: Significa que 20 estudiantes obtuvieron un puntaje mayor o igual a 75 y menor 81 puntos 57: Significa que 57 estudiantes obtuvieron un puntaje menor a 81 puntos 43: Significa que 43 estudiantes obtuvieron un puntaje mayor o igual que 75 puntos 25: Significa que el 25% de los estudiantes obtuvieron un puntaje mayor o igual a 75 y menor a 81 puntos 71.25: Significa que el 71.25% de los estudiantes obtuvieron un puntaje menor que 81 puntos 53.75: Significa que el 53.75% de los estudiantes obtuvieron un puntaje mayor o igual que 75 puntos |
REPRESENTACIÓN GRÁFICA DE
HISTOGRAMAS DE FRECUENCIAS
Y ALGUNAS INTERPRETACIONES
HISTOGRAMAS DE FRECUENCIAS
Y ALGUNAS INTERPRETACIONES
El histograma de frecuencias es un gráfico de área, que tiene por objetivo mostrar la forma de la distribución de los datos. Está compuesto por rectángulos, uno para cada intervalo, unidos por sus lados entre si; la base de los rectángulo está determinada por la amplitud del intervalo de clase y la altura por la frecuencia absoluta o la relativa.
Cuando se representa en el gráfico las frecuencias absolutas, la suma de las áreas de los rectángulos debe ser igual al total de las observaciones. Cuando se representa en el gráfico las frecuencias relativas, la suma de las áreas de los rectángulos debe ser igual a uno o a 100 cuando están expresadas en porcentaje.
Histograma de frecuencias absolutas
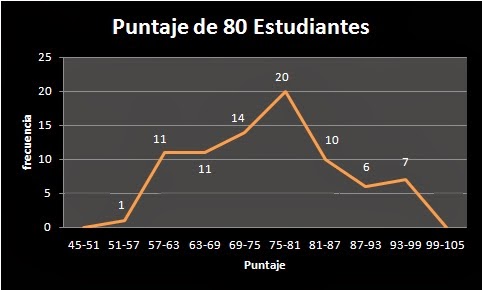
Hay 20 estudiantes con un puntaje mayor o igual a 75 y menor que 81 puntos
Polígono de frecuencias absolutas
Histograma de frecuencias relativas
Histograma de frecuencias relativas acumuladas menor que
Ojiva relativa menor que
Histograma de frecuencias relativas acumuladas Mayor que
Ojiva relativa Mayor que
El 53.75 % de los estudiantes obtuvieron un puntaje mayor o igual a 75 puntos
|
EJEMPLO DE CONTEO DE DATOS MEDIANTE EL USO DE EXCEL
EJERCICIOS DE REPASO
 DATOS CUALITATIVOS
DATOS CUALITATIVOS

Para cada conjunto de datos dado construir:
a) La distribución de frecuencias absolutas
b) La distribución de frecuencias relativas
c) La distribución de frecuencias absolutas acumuladas
d) La distribución de frecuencias relativas acumuladas
e) Diagrama de barras
f) Diagrama circular.
1. Estudio hecho a un grupo de estudiantes sobre su grupo sanguíneo.
A
|
B
|
O
|
A
|
B
|
AB
|
A
|
O
|
O
|
O
|
O
|
O
|
A
|
O
|
A
|
O
|
B
|
O
|
A
|
B
|
2. Estado civil de un grupo de personas de una empresa
S
|
C
|
D
|
C
|
S
|
C
|
UL
|
S
|
S
|
C
|
D
|
S
|
C
|
UL
|
S
|
V
|
C
|
D
|
V
|
C
|
UL
|
S
|
UL
|
S
|
C
|
D
|
C
|
D
|
S
|
C
|
S=Soltero C=Casado UL=Unión Libre D=Divorciado V=Viudo
3. Encuesta realizada a un grupo de estudiantes sobre cuáles son los libros que mas les gusta leer:
Tipo de libro
|
Alumnos
|
Porcentaje
|
Grados
|
POESÍA
|
12
| ||
TERROR
|
24
| ||
AVENTURAS
|
30 %
| ||
MISTERIO
| |||
TEATRO
|
12
| ||
TOTAL
|
90
|
4. Color de los carros en un parqueadero.
NEGRO
|
BLANCO
|
ROJO
|
AZUL
|
AMARILLO
|
BLANCO
|
AMARILLO
|
BLANCO
|
VERDE
|
BLANCO
|
AZUL
|
AZUL
|
ROJO
|
NEGRO
|
ROJO
|
VERDE
|
ROJO
|
NEGRO
|
ROJO
|
NEGRO
|
ROJO
|
NEGRO
|
AZUL
|
AMARILLO
|
AZUL
|
AMARILLO
|
BLANCO
|
VERDE
|
NEGRO
|
BLANCO
|
EJERCICIOS DE REPASO
 DATOS CUANTITATIVOS
DATOS CUANTITATIVOS

Para cada conjunto de datos dado:
a) Hallar la distribución de frecuencias absolutas
b) Hallar la distribución de frecuencias relativas
c) Hallar la distribución de frecuencias absolutas acumuladas
d) Hallar la distribución de frecuencias relativas acumuladas
e) Hallar la media, la mediana y la moda
e) Hallar la media, la mediana y la moda
f) Construir un Histograma de frecuencias
1. Estatura en centímetros de un grupo de estudiantes.
1. Estatura en centímetros de un grupo de estudiantes.
175
|
173
|
181
|
169
|
195
|
196
|
177
|
174
|
170
|
168
|
185
|
173
|
170
|
168
|
172
|
179
|
184
|
183
|
176
|
188
|
179
|
177
|
172
|
180
|
193
|
195
|
178
|
187
|
190
|
192
|
188
|
180
|
172
|
169
|
171
|
176
|
184
|
183
|
180
|
179
|
2. Registro de los saldos de 40 cuentas de ahorros que se abrieron el último mes en Bancafé, en miles de pesos.
179.80
|
112.17
|
1150.00
|
100.00
|
1009.10
|
1212.43
|
470.53
|
780.00
|
352.00
|
1595.10
|
890.00
|
1200.00
|
1482.00
|
695.15
|
952.51
|
510.52
|
783.00
|
793.10
|
937.01
|
217.00
|
712.10
|
293.00
|
579.00
|
287.00
|
1112.52
|
1394.05
|
1101.00
|
501.01
|
711.41
|
1202.00
|
415.00
|
602.02
|
1312.52
|
1175.00
|
783.00
|
1390.00
|
666.66
|
155.10
|
1422.03
|
1273.01
|
3. Ingreso de un grupo de comerciantes (en miles de pesos)
1380
|
1380
|
889
|
1030
|
1050
|
1180
|
997
|
1201
|
920
|
783
|
709
|
883
|
842
|
900
|
1000
|
950
|
970
|
990
|
1273
|
753
|
1350
|
1290
|
815
|
1250
|
712
|
850
|
797
|
1153
|
1080
|
1300
|
4. Presupuesto de viáticos por concepto de transporte de un grupo de empleados de una empresa (En miles de pesos)
51.02
|
99.99
|
73.99
|
79.99
|
80.00
|
63.09
|
71.11
|
58.73
|
61.11
|
72.14
|
83.21
|
50.00
|
70.00
|
60.00
|
65.72
|
69.99
|
57.03
|
92.29
|
60.00
|
89.49
|
81.00
|
82.22
|
59.99
|
89.99
|
90.00
|
79.82
|
77.77
|
89.99
|
80.00
|
69.99
|
5. Tiempos (en minutos) que tardan 30 estudiantes en terminar un parcial de estadística
42.3
|
67.7
|
53.3
|
63.9
|
70.1
|
70.0
|
52.6
|
61.9
|
41.7
|
39.2
|
37.2
|
63.2
|
45.7
|
38.9
|
68.3
|
69.2
|
39.2
|
42.7
|
52.4
|
52.5
|
41.9
|
58.9
|
69.1
|
68.3
|
64.9
|
39.2
|
45.5
|
55.5
|
61.2
|
69.8
|
ADELANTE
|














No hay comentarios.:
Publicar un comentario